金价历史趋势_金价历史回顾论文

1.国际石油价格的波动对我国国内能源市场的影响

2.白银涨价了吗

3.大卫 李嘉图在经济学上有什么成就？

4.一元线性回归模型是不是太简单了？可以预测房价吗？金价呢？如果不行还有什么比较简单的模型可以。。

5.论文:原油价格上涨和股票市场的关系

6.现代数学方法概论论文

国际石油价格的波动对我国国内能源市场的影响

字数多了，贴不下了，你去看看原文吧

二、长期石油政策抉择和金融博弈

石油作为一种关系到国计民生的重要战略,历来是影响各国乃至世界经济发展的重要因素之一。尤其是当今世界经济处于经济调整的复苏阶段,各国经济结构和产业结构的转折、更新,进一步扩大了对国际石油的需求,其中一些新兴市场国家和地区的经济快速发展和经济升级周期,更加大了对石油能源的需求。由此可以看出石油价格的重要性。如果石油价格过高,将促使生产成本上升、物价上升,直接制约经济的发展速度；反之,如果油价过低,将使石油出口国的外汇收入大大减少,从而损害了石油出口国的经济利益；因此,中期看,如何将国际石油价格维持在一个合理的水平,是国际社会需要妥善解决的一个重大问题。

1、世界经济增长的不确定性。国际石油价格持续上涨是世界经济进一步增长的不确定因素。据国际货币基金组织估计,国际石油价格每桶上涨5美元,1年内世界经济的增长速度将下降0.3个百分点。石油生产和价格涨跌是一个周期性问题,并且会影响不同类型国家的经济增长。国际油价处于高位时会导致石油生产过剩、供过于求,继之价格又会暴跌,由此又导致石油生产收缩,石油价格上涨,这已经是由历史证明的经验。因此,有关国家经济增长不能不受这种石油生产------价格周期的影响,相比之下,石油输入国将比较出口国更易受到这种经济周期波动的冲击。目前工业发达国家经济复苏对石油的需求也有增无减,石油是发达国家最重要的进口项目,并且是对外贸易中最大的逆差项目。国际石油价格的波动对于严重依赖进口的欧元区国家所产生的影响将最为直接,欧元贬值最为重要的原因之一就在于国际石油价格上涨所造成的欧元区通货膨胀上升的压力。即使由于石油输出国增产,使涨价问题一时得到缓解,也不可能改变这一基本走势。

从发展中国家看,近年来亚洲经济复苏势头比较好,扩大了对石油供给的需求。1990--1999年期间,除西亚产油国外,亚洲东部国家的石油需求增幅约占全球石油需求增幅的80%；如果油价居高不下,将对亚洲国家的财政收支、通货膨胀、国际贸易收支、偿还外债能力等都形成较大的压力,影响亚洲经济继续增长的良好势头。北美、欧洲和亚洲是世界的三大石油市场,其中亚洲的石油需求增长速度最快,但是作为亚洲主要产油国的产油量却基本上没有增长,这使亚洲各国从中东的石油进口量大幅度上升。另外,主要产油的发展中国家和地区的政治、经济动荡性也直接影响着油价的波动上涨,如委内瑞拉的政治问题使石油减产严重,沙特阿拉伯经济引起的设备老化石油减产,以及伊拉克破坏性的石油状况,都是油价潜在波动隐患。在产油国中,一些严重依赖石油收入拉动经济的发展中国家或经济转轨国家,如俄罗斯等,受到石油价格波动的影响较大,涨价使之大喜,跌价则大悲。2003年以来国际石油价格的上涨已经在很大程度上制约了世界经济的总体复苏态势和增长水平。随着伊拉克紧张局势因突发暴力再度恶化,国际油价的高企可能成为世界经济复苏的障碍。

2、能源需求结构调整的必然性。伴随经济全球化、生产力的迅速发展,各国国民经济实力的快速增强以及经济增长质量提高,各国对能源的需求越来越大,2004年世界石油需求每日增加165万桶,石油日消费量达到7990万桶。同时,国际能源需求的结构正在发生根本性变化,世界原油库存在减少,石油开的、技术与设备综合问题凸显；还有燃煤需求有所下降,燃油及燃气需求迅速增长,从而使国际燃油供需矛盾越来越突出；随着新经济高科技含量的增加,国际石油生产、运输、储存等也有高新技术的更新改造,替代石油以及原油组合也逐渐显现,天然气、氢气等能源开发也对国际石油供求格局具有影响。由于世界经济面临传统经济转向新经济的转换,特别是出口拉动转向投资带动的结构转型,各国内需的扩大不仅增加了投资需求,也促使国际原材料价格急剧上涨,石油与钢铁、煤炭等原材料的上涨便具有连带反应。全球化商品流动时代使国际石油市场出现运输瓶颈和储存技术难题,运输成本的高企、港口和道路拥挤、储存成本上升都在一定程度上刺激了油价进一步上扬。

美国能源署预计,全球对各种形式能源的需求将在今后20年中增长54%,仅原油日消费量就将可能增长至4000万桶；美国能源资料协会(EIA)的2025年远景预测还显示,发展中国家能源使用增长将最为强劲,尤其是中国和印度,因经济颇具活力将进一步加大能源需求。预计今后20年中,发展中国家的能源使用量将锐增91%,而工业化国家用量将增长33%。2025年全球石油需求预计将增至每日1.21亿桶,2004年为每日8100万桶。美国、中国以及亚洲其它发展中国家将消化近六成的新增原油。有数据显示,亚洲2004年的能源需求将增长8%-10%,石油对经济增长的支持作用不言而喻。

3、国际经济关系的协调性。石油问题在国际经济关系中具有多层面的复杂性,比如OPEC与非OPEC之间的矛盾,石油供给国与需求国之间的矛盾,进而延展至大国与大国、强国与强国、富国与富国、大国与小国、富国与穷国等不同层次的复杂协调合作关系。国际石油价格不确定的波动干扰了世界经济的复苏,增加了主要国家和地区的经济政策协调的难度。国际石油问题引发的国际经济关系中石油产出和需求的关系变异,聚焦在金融安全与经济利益,石油问题成为国别关系强化与松散、重组与离合的重要筹码,其中主导的突出影响因素是美国经济利益、政治霸权、军事强权及其在金融市场中独特地位。石油问题是美国对外政治、贸易、经济与外交关系的主线,也是美欧日经济金融竞争与较量的主要战线之一。统计数据显示,美国从中东的石油进口占其石油进口总量的25%,欧洲占60%,日本占80%,美欧日三大利益集团竞争源于石油,又怨于石油。

世界经济发展供求格局的日益明显,发达国家是主要石油消费国,而大部分石油出口集中在一些发展中国家和经济转轨国家,这里既相互需要,又相互矛盾,是一种需要不断调整和协调的关系。此外,美俄、日俄、中俄、中日以及新老欧洲之间的多重和复杂的国际关系均有石油色彩的渗入,政治意图也已成为油价波动的重要诱因。特别是俄罗斯与西方一些大国的利益交错,其中既有西方对外扩展与俄罗斯深化利益需求的意图,也有西方对俄罗斯石油需求的战略意图,日本的西伯利亚输油管线举动已经显为人知,美国更是谋划长远。

从地域角度看,海湾石油是工业发达国家所用石油的主要依托点。因此,世界舞台上的国际力量都紧紧盯住海湾巨大的石油储量,巴以冲突不断、海湾战事连连,也就不难寻味。海湾石油是世界经济和政治问题的焦点之一,它的起伏跌宕预示着国际局势的发展趋势。美国对伊拉克战争结束之后,预测国际石油前景将更为困难,战事对石油市场影响超出预期。2004年政治因素将对石油价格起主导作用,随着政治问题的化解减弱和积聚增强,油价波动继续扩大。

4、全球化和区域化的差异性。自欧元问世以来,对欧元的排挤和打击一直是美国国际金融战略的主旨,有形和无形较量已经使欧元承受了巨大的压力与风险。美欧根本性的差异对立在于全球化与区域化理念的博弈。美日是经济全球化的极力推崇者,因为美日经济规模与市场份额和发展水平的主导,使他们在本地区内难以与弱势的广展中国家或新兴市场经济体相融合,担心在区域化中付出"代价",他们必然以全球化显示其优势并巩固其利益,；而欧洲则是政治、经济、金融和贸易等相对均衡的发达国家经济体,具有实现区域化的先天优势,欧盟5月1日东扩10国的实现,使新老欧洲的融合形成更强大的经济联合体,无论经济、人口或市场已经超出美国。美日和欧洲之间全球化利益主导和区域化利益差异,以及不均衡和均衡的状况,是形成各自经济全球化和欧洲经济区域化理念不同的主要原因。美欧日经济金融理念的差异也反映在金融市场汇率、股价、金价或油价等价格竞争中。在国际石油的争夺上,三大经济体或货币体也必然会以各自经济全球化或区域化理念,加大国际产品的竞争。以科索沃和阿富汗、伊拉克战争冲击原来的石油供求格局,辅之以货币竞争,则是不可忽视的美国全球化战略意向。从日本看,为弥补自身石油需求,其加紧与亚洲、中东国家的经贸合作,改善甚至强化与俄罗斯的关系,其动向也值得揣摩和研究。

特别需要指出的是,国际石油价格走势已经超出市场相对乐观平和的预期,石油作为政治战略筹码的用途大有提升,并潜藏有美国等大国金融战略的策划。美国可以运用美元报价体系的优势,以美元挂钩石油报价手段控制油价,并伴之石油储存的策略,进一步显示其全球石油战略和金融战略的综合优势。

[对策]国际油价走势与我国石油战略

国际石油价格因全球经济复苏需求而扩大,因产油国政策调整而紧张,因地缘政治因素而恶化,因季节因素而变化,未来前景不容乐观。无论如何,石油持续走高必然影响世界经济增长。预计国际石油市场价格趋势短期内难以稳定向下,中期将会继续持续高企。因此,2004年的国际石油价格高点将会突破40美元乃至45美元,全年石油平均水平将可能达到35美元左右,高于去年31美元的平均价；如果国际石油价格一段时间维持35-40美元的高位,世界经济增长至少有0.2个百分点的减值；未来2-3年,国际石油价格将继续在涨跌中高企,但年平均价格有可能在33-38美元区间波动。对于世界经济而言,金融风险与石油危机都不可掉以轻心,更值得关注与防范因石油价格变化所引发的国际金融风险,包括美元动荡性风险和欧洲货币潜在的危机风险,这两大货币汇率走势与石油价格水平直接联系,必将影响全球经济、金融、贸易和投资等相关层面的变化与调整。今年以来已经召开和即将再聚会的G-7,都一直关注石油与汇率问题,突出表明了石油与金融安全的必然联系和重要影响。而全球利率上调的动向,将会进一步加大国际金融市场与国际石油市场联动效应。

我国是国际石油市场一个新兴的战略因素。扩大石油进口成为国际石油价格的一个重要影响。随着经济持续增长,我国已经成为石油需求大国,去年进口石油达到9941万吨,今年可能达到1.1亿至1.2亿吨,这也是4年来世界石油消费量的最高点。近期国际能源署的预测指出,中国石油需求增长将继续超出预期,为高企的国际油价提供支撑。国际能源署将我国2004年第一季石油日需求量上调18万桶,至614万桶,较去年同期增长18%。目前中国是仅次于美国的全球第二大石油消费国,2003年原油及油品进口量平均为每日210.6万桶。我国2月石油日进口量猛增至创纪录的316.2万桶,比1月高28.3万桶。我国海关总署的统计数据显示,我国2004年前3个月的原油进口量达3014万吨,较上年同期飙升35.7%。而OPEC在近期的月度报告中也指出,由于中国经济高速发展,OPEC将提高2004年度的世界石油消费量预期,2004年世界石油消费量预期由原来的每天2387万桶提高到2617万桶。

在我国能源消费开始对国际能源市场产生重要影响的同时,国际油价的波动也导致了我国国内的油价波动。我国从1998年开始对国内成品油市场实行动态管理,即根据国际市场上原油价格的涨跌来调整国内的成品油价格。国际市场油价的巨幅波动,不仅影响石油及上下游企业的经营绩效,加大了相关企业的经营难度,同时也对我国经济的走向,特别是价格走向产生广泛影响。有鉴于此,我们应当加快实施"国家石油储备战略",开展石油期货交易,完善国内成品油市场的价格形成与调整机制,维护我国的石油安全和金融安全,以确保国民经济健康稳定地发展。

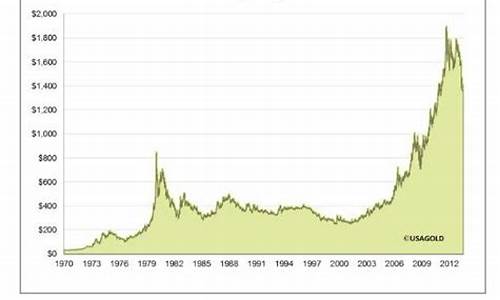
白银涨价了吗

白银涨价了。从历史上看,白银一般在金价开始上涨后的6至12个月内反弹。黄金与白银比率的最大爆发点一般出现在黄金价格上涨速度比白银高出30%至60%的时候。换句话说,当黄金与白银的相对价格出现重大差异时,白银会涨得更高,从而导致金银比下降。

白银的历史：

1、在古代，人类就对银有了认识。银和黄金一样，是一种应用历史悠久的贵金属，至今已有4000多年的历史。由于银独有的优良特性，人们曾赋予它货币和装饰双重价值，英镑和我国解放前用的银元，就是以银为主的银、铜合金。在我国清代，1两银子约相当于今天的400-500元人民币（长美注）。

2、而银比金活泼，虽然它在地壳中的丰度大约是黄金的15倍，但它很少以单质状态存在，因而它的发现要比金晚。在古代，人们就已经知道开银矿，由于当时人们取得的银的量很小，使得它的价值比金还贵。公元前1780至1580年间，埃及王朝的法典规定，银的价值为金的2倍，甚至到了17世纪，日本金、银的价值还是相等的。银最早用来做装饰品和餐具，后来才作为货币。

白银，即银，因其色白，故称白银，与黄金相对。多用其作货币及装饰品。古通货时称白银。银，永远闪耀着月亮般的光辉，银的论文原意，也就是“明亮”的意思。我国也常用银字来形容白而有光泽的东西，如、银杏、银鱼、银耳、银幕等。

3、我国古代常把银与金铜并列，称为“唯金三品”。《禹贡》一书便记载着“唯金三品”，可见我国早在公元前二十三世纪，即距今四千多年前便发现了银。在大自然中，银常以纯银的形式存在，人们便曾找到一块重达13.5吨的纯银！另外，也有以氯化物与硫化物的形式存在，常同铅、铜、锑、砷等矿石共生在一起。

大卫 李嘉图在经济学上有什么成就？

《政治经济学及赋税原理》以精炼的理论架构，贴近现实的语言与例证，全面论述了他所生活的那个年代资本主义生产方式的运行机制，使他成为了英国古典政治经济学的集大成者，19世纪初叶最伟大的经济学家。

1809年至1815年，他在经济学领域发表一系列论文，探索货币问题，从而成为一位权威的货币理论家。 1815年 2月，他发表《论谷物低价格对资本利润的影响》，初步阐述了地租、利润、工资问题，并力主自由贸易和废除谷物法。这种观点代表了上升的英国工业资产阶级的利益和要求。

李嘉图在1817年出版了《政治经济学和赋税原理》这部著作，集中反映他的经济学理论。在价值学说方面，他继承了斯密对使用价值和交换价值的区分，但批判了斯密认为有些商品没有使用价值也有交换价值的论点，认为任何商品没有效用就不会有交换价值。

在价值量的决定问题上，他批判了斯密的价值决定于耗费劳动又决定于购买劳动的观点，正确指出两者并不相等，购买劳动不能决定价值，只能由耗费劳动决定价值，商品价值和生产商品所消耗的劳动量成正比。

书中还批判了斯密的价值由工资、利润、地租决定的错误观点，正确指出价值还包含制造工具所耗费的劳动。这是李嘉图价值学说的一个新贡献。从此，他成了政治经济学的理论权威，逐渐形成了“李嘉图学派”。

1810年，李嘉图被选为国会议员，他主张进行选举改革、实现言论、结社和集会自由，反对1819年反民主法令。

李嘉图在《政治经济学及赋税原理》中辟出专章，集中讨论了国际贸易问题，提出了著名的比较优势贸易理论。

扩展资料

大卫·李嘉图继承和发展了亚当·斯密创立的劳动价值理论，并以此作为建立比较优势理论的理论基础。

在分析论述比较优势理论中，李嘉图赋予劳动以重要的地位，他在《政治经济学及赋税原理》中开宗明义就指出，“一件商品的价值，或曰用以与之交换的任何其他商品的数量，取决于生产此件商品所必需的相对劳动量。”

进而，他也像斯密一样，将价值区分为“使用价值”和“交换价值”，指出“有用性不是衡量交换价值的标准”，认为“商品的交换价值以及决定商品交换价值的法则，即决定为了交换他种商品必须付出多少此种商品的规律，全然取决于在这些商品上所付出的相对劳动量”。

参考资料百度百科——李嘉图

一元线性回归模型是不是太简单了？可以预测房价吗？金价呢？如果不行还有什么比较简单的模型可以。。

一元线性回归模型预测房价和金价，那是天方夜谭了，完全不靠谱的。房价和进价的影响因素成千上万，怎么能用一元回归模型？如果这样可以那一元回归模型就可以预测股票价格了。

就金价来说，可以单独考察金价与金产量的关系，这勉强可以用一元回归模型。

论文:原油价格上涨和股票市场的关系

1000字有点多！

其实根本原因说明白了就几句话。目前工业生产和人们日常生活都非常需要石油。石油贵了，工业产品自然也就贵了，就是所谓的PPI（生产者价格指数）就高；石油贵了人们日常生活的开支也大了，也就是所谓的CPI（消费者价格指数）高了。PPI提高还会带动CPI提高。CPI提高了就是通货膨胀了，巴菲特说过“通货膨胀是企业最大的敌人。”企业的利润降低了，自然他的股票价格就会跟着降低。

具体的问题要说明白太费劲了。随便说说。

现代数学方法概论论文

现代数学方法概论论文

经济数学问题例说自1993年5月高考命题组提请注意数学的应用以后，1995年全国高考文理科试题中又出现了一道关于淡水鱼养殖的市场预测的应用题，这是一道数学应用方面的好题，由于它是经济数学方面的问题，从而在建立社会主义市场经济新体制的今天，格外地引起大家的注目。

所谓经济数学问题，就是用数学方法来研究经济学的一些问题，如经济增长率、人口增长率等方面的国民经济问题，银行业务问题，证券市场问题，保险计算问题，消费与市场预测问题，投入产出问题，等等。上述问题中，能用中学生可以接受的初等数学方法解决的一些基础问题都应当引起我们的重视。

下面举几个例子。

例1：某商品的市场需求量P（万件）?、市场供应量Q与市场价格x（元／件）分别近似地满足下列关系： P＝－x＋70； Q＝2x－20当P＝Q时的市场价格称为市场平衡价格，此时的需求量称为平衡需求量。

（1）求平衡价格和平衡需求量；

（2）若每件商品征税3元，求新的平衡价格；

（3）若要使平衡需求量增加4万件，对每件商品应给予多少元补贴？

解：（1）求得平衡价格为30元/件，平衡需求量为40万件。

（2）设新的市场平衡价格为x元/件，此即为消费者支付价格，而提供者得到的价格则为（x一3）元/件，依题意得－x＋70＝2（x－3）－20，从而解得新的平衡价格为32元/件。

（3）设给予t元/件补贴，此时的市场平衡价格亦即消费者支付价格为x元/件，则提供者收到的价格为（x＋t）元/件，依题意得方程组－x＋70＝44

2（x＋t）－20＝44　解之得 x＝26 t＝6

例2：某产品日产量为20台，每台价90元，若日产量每增加1台，则单价就要降低3元，问如何设计生产，使日总收入最大？

解：设每日多生产x台，总收入为y元，依题意得 y＝（90－3x）（20＋x）易得当日产量为25台时，总收入最大。

例3：某厂今年初100万元，复利计息，年利率为10％（即本年的利息计入次年的本金生息），计算从今年末开始每年偿还固定的金额，恰在第12年末还清，问每年偿还的金额是多少万元？

解：设每年偿还的金额为X万元，依题意得： x＋x（1＋10％）＋x（1＋10％）2＋…＋x（1＋10％）11＝100（1＋10％）12解之得x＝15（万元）

09-12-18 | 添加评论 | 打赏

0

hellomydram11

例如：

极限的求法

1. 直接代入法

适用于分子,分母的极限不同时为零或不同时为

例 1. 求 .

分析 由于 ,

所以用直接代入法.

解 原式=

2.利用极限的四则运算法则来求极限

为叙述方便,我们把自变量的某个变化过程略去不写,用记号表示在某个极限过程中的极限,因此极限的四则运算法则可确切地叙述如下:

定理 在同一变化过程中,设都存在,则

(1)

(2)

(3)当分母时,有

总的说来,就是函数的和,差,积,商的极限等于函数极限的和,差,积,商.

求.

解

3.无穷小量分出法

适用于分子,分母同时趋于 ,即 型未定式

例3.

分析 所给函数中,分子,分母当 时的极限都不存在,所以不能直接应用法则.注意到当 时,分子,分母同时趋于 ,首先将函数进行初等变形,即分子,分母同除 的最高次幂,可将无穷小量分出来,然后再根据运算法则即可求出极限.

为什么所给函数中,当 时,分子,分母同时趋于 呢 以当 说明:因为 ,但是 趋于 的速度要比 趋于 的速度快,所以 .不要认为 仍是 (因为 有正负之分).

解 原式 (分子,分母同除 )

(运算法则)

(当 时, 都趋于 .无穷大的倒数是无穷小.)

4. 消去零因子法

适用于分子,分母的极限同时为0,即 型未定式

例4.

分析 所给两个函数中,分子,分母的极限均是0,不能直接使用法则四,故用消去零因子法.

解 原式= (因式分解)

= (约分消去零因子 )

= (应用法则)

=

5. 利用无穷小量的性质

例5. 求极限

分析 因为 不存在,不能直接使用运算法则, 故必须先将函数进行恒等变形.

解 原式= (恒等变形)

因为 当 时, , 即 是当 时的无穷小,而 ≤1, 即 是有界函数,由无穷小的性质:有界函数乘无穷小仍是无穷小,

得 =0.

6. 利用拆项法技巧

例6:

分析:由于=

原式=

7. 变量替换

例7 求极限 .

分析 当 时,分子,分母都趋于 ,不能直接应用法则,注意到 ,故可作变量替换.

解 原式 =

= (令 ,引进新的变量,将原来的关于 的极限转化为 的极限.)

= . ( 型,最高次幂在分母上)

8. 分段函数的极限

例8 设 讨论 在点 处的极限是否存在.

分析 所给函数是分段函数, 是分段点, 要知 是否存在,必须从极限存在的充要条件入手.

解 因为

所以 不存在.

注1 因为 从 的左边趋于 ,则 ,故 .

注2 因为 从 的右边趋于 ,则 ,故 .

宏志网校 俊杰

1、利用定义求极限。

2、利用柯西准则来求。 柯西准则：要使{xn**有极限的充要条件使任给ε>0,存在自然数N，使得当n>N时，对于 任意的自然数m有|xn-xm|<ε.

3、利用极限的运算性质及已知的极限来求。 如：lim(x+x^0.5)^0.5/(x+1)^0.5 =lim(x^0.5)(1+1/x^0.5)^0.5/(x^0.5)(1+1/x)^0.5 =1.

4、利用不等式即：夹挤定理。

5、利用变量替换求极限。 例如lim (x^1/m-1)/(x^1/n-1) 可令x=y^mn 得：＝n/m.

6、利用两个重要极限来求极限。 （1）lim sinx/x=1 牐爔->0 (2)lim (1+1/n)^n=e 牐爊->∞ 7、利用单调有界必有极限来求。

8、利用函数连续得性质求极限。

9、用洛必达法则求，这是用得最多的。

10、用泰勒公式来求，这用得也很经常。

　按一定次序排列的一列数称为数列（sequence of number）。数列中的每一个数都叫做这个数列的项。排在第一位的数列称为这个数列的第1项（通常也叫做首项），排在第二位的数称为这个数列的第2项……排在第n位的数称为这个数列的第n项。所以，数列的一般形式可以写成

a1，a2，a3，…，an，…

简记为｛an｝，项数有限的数列为“有穷数列”（finite sequence），项数无限的数列为“无穷数列”（infinite sequence）。

从第2项起，每一项都大于它的前一项的数列叫做递增数列；

从第2项起，每一项都小于它的前一项的数列叫做递减数列；

从第2项起，有些项大于它的前一项，有些项小于它的前一项的数列叫做摆动数列；

各项呈周期性变化的数列叫做周期数列（如三角函数）；

各项相等的数列叫做常数列。

通项公式：数列的第N项an与项的序数n之间的关系可以用一个公式表示，这个公式就叫做这个数列的通项公式。

数列中数的总数为数列的项数。特别地，数列可以看成以正整数集N*（或它的有限子集｛1，2，…，n｝）为定义域的函数an=f(n)。

如果可以用一个公式来表示,则它的通项公式是a(n)=f(n).

[编辑本段]表示方法

如果数列｛an｝的第n项与序号n之间的关系可以用一个式子来表示，那么这个公式叫做这个数列的通项公式。如an=(-1)^(n+1)+1

如果数列｛an｝的第n项与它前一项或几项的关系可以用一个式子来表示，那么这个公式叫做这个数列的递推公式。如an=2a(n-1)+1 (n>1)

[编辑本段]等差数列

定义

一般地，如果一个数列从第2项起，每一项与它的前一项的差等于同一个常数，这个数列就叫做等差数列（arithmetic sequence），这个常数叫做等差数列的公差（common difference），公差通常用字母d表示。

缩写

等差数列可以缩写为A.P.（Arithmetic Progression）。

等差中项

由三个数a，A，b组成的等差数列可以堪称最简单的等差数列。这时，A叫做a与b的等差中项（arithmetic mean）。

有关系：A＝（a＋b）/2

通项公式

an=a1+(n-1)d

an=Sn-S(n-1) (n>=2)

前n项和

Sn=n(a1+an)/2=n*a1+n(n-1)d/2

性质

且任意两项am，an的关系为：

an=am+(n-m)d

它可以看作等差数列广义的通项公式。

从等差数列的定义、通项公式，前n项和公式还可推出：

a1+an=a2+an-1=a3+an-2=…=ak+an-k+1，k∈{1,2,…,n}

若m，n，p，q∈N*，且m+n=p+q，则有

am+an=ap+aq

Sm-1=(2n-1)an，S2n+1=(2n+1)an+1

Sk，S2k-Sk，S3k-S2k，…，Snk-S(n-1)k…或等差数列，等等。

和＝（首项＋末项）×项数÷2

项数＝（末项-首项）÷公差＋1

首项=2和÷项数-末项

末项=2和÷项数-首项

设a1,a2,a3为等差数列。则a2为等差中项,则2倍的a2等于a1+a3，即2a2=a1+a3。

应用

日常生活中，人们常常用到等差数列如：在给各种产品的尺寸划分级别

时，当其中的最大尺寸与最小尺寸相差不大时，常按等差数列进行分级。

若为等差数列，且有an=m,am=n.则a(m+n)＝0。

[编辑本段]等比数列

定义

一般地，如果一个数列从第2项起，每一项与它的前一项的比等于同一个常数，这个数列就叫做等比数列（geometric sequence）。这个常数叫做等比数列的公比（common ratio），公比通常用字母q表示。

缩写

等比数列可以缩写为G.P.（Geometric Progression）。

等比中项

如果在a与b中间插入一个数G，使a，G，b成等比数列，那么G叫做a与b的等比中项。

有关系：G^2＝ab；G＝±(ab)^(1/2)

注：两个非零同号的实数的等比中项有两个，它们互为相反数，所以G^2=ab是a,G,b三数成等比数列的必要不充分条件。

通项公式

an=a1q^(n-1)

an=Sn-S(n-1) (n≥2)

前n项和

当q≠1时，等比数列的前n项和的公式为

Sn=a1(1-q^n)/(1-q)=(a1-an*q)/(1-q) (q≠1)

性质

任意两项am，an的关系为an=am·q^(n-m)

（3）从等比数列的定义、通项公式、前n项和公式可以推出： a1·an=a2·an-1=a3·an-2=…=ak·an-k+1，k∈{1,2,…,n}

（4）等比中项：aq·ap=ar*2，ar则为ap，aq等比中项。

记πn=a1·a2…an，则有π2n-1=(an)2n-1，π2n+1=(an+1)2n+1

另外，一个各项均为正数的等比数列各项取同底数数后构成一个等差数列；反之，以任一个正数C为底，用一个等差数列的各项做指数构造幂Can，则是等比数列。在这个意义下，我们说：一个正项等比数列与等差数列是“同构”的。

性质：

①若 m、n、p、q∈N*，且m＋n=p＋q，则am·an=ap·aq；

②在等比数列中，依次每 k项之和仍成等比数列.

“G是a、b的等比中项”“G^2=ab（G≠0）”.

(5) 等比数列前n项之和Sn=A1(1-q^n)/(1-q)

在等比数列中，首项A1与公比q都不为零.

注意：上述公式中A^n表示A的n次方。

应用

等比数列在生活中也是常常运用的。

如：银行有一种支付利息的方式---复利。

即把前一期的利息赫本金价在一起算作本金，

在计算下一期的利息，也就是人们通常说的利滚利。

按照复利计算本利和的公式：本利和=本金*(1+利率)^存期

如果一个数列从第2项起，每一项与它的前一项的比等于同一个常数，这个数列就叫做等比数列。这个常数叫做等比数列的公比，公比通常用字母q表示(q≠0)。

（1）等比数列的通项公式是：An=A1*q^（n－1）

若通项公式变形为an=a1/q*q^n(n∈N*),当q＞0时，则可把an看作自变量n的函数，点(n,an)是曲线y=a1/q*q^x上的一群孤立的点。

（2）求和公式：Sn=nA1(q=1)

Sn=A1(1-q^n)/(1-q)

=(a1-a1q^n)/(1-q)

=a1/(1-q)-a1/(1-q)*q^n ( 即A-Aq^n)

(前提：q不等于 1)

任意两项am，an的关系为an=am·q^(n-m)

（3）从等比数列的定义、通项公式、前n项和公式可以推出： a1·an=a2·an-1=a3·an-2=…=ak·an-k+1，k∈{1,2,…,n}

（4）等比中项：aq·ap=ar^2，ar则为ap，aq等比中项。

记πn=a1·a2…an，则有π2n-1=(an)2n-1，π2n+1=(an+1)2n+1

另外，一个各项均为正数的等比数列各项取同底数后构成一个等差数列；反之，以任一个正数C为底，用一个等差数列的各项做指数构造幂Can，则是等比数列。在这个意义下，我们说：一个正项等比数列与等差数列是“同构”的。

[编辑本段]一般数列的通项求法

一般有：

an=Sn-Sn-1 （n≥2）

累和法（an-an-1=... an-1 - an-2=... a2-a1=...将以上各项相加可得an）。

逐商全乘法（对于后一项与前一项商中含有未知数的数列）。

化归法（将数列变形，使原数列的倒数或与某同一常数的和成等差或等比数列）。

特别的：

在等差数列中，总有Sn S2n-Sn S3n-S2n

2(S2n-Sn)=(S3n-S2n)+Sn

即三者是等差数列,同样在等比数列中。三者成等比数列

不动点法（常用于分式的通项递推关系）

[编辑本段]特殊数列的通项的写法

1,2,3,4,5,6,7,8....... ---------an=n

1,1/2,1/3,1/4,1/5,1/6,1/7,1/8......-------an=1/n

2，4，6，8，10，12，14.......-------an=2n

1,3,5,7,9,11,13,15.....-------an=2n-1

-1,1,-1,1,-1,1,-1,1......--------an=(-1)^n

1,-1,1,-1,1,-1,1,-1,1......--------an=(-1)^(n+1)

1,0,1,0,1,0,1,01,0,1,0,1....------an=[(-1)^(n+1)+1]/2

1,0,-1,0,1,0,-1,0,1,0,-1,0......-------an=cos(n-1)π/2=sinnπ/2

9,99,999,9999,99999,......... ------an=（10^n)-1

1,11,111,1111,11111.......--------an=[（10^n)-1]/9

1，4，9，16，25，36，49，.......------an=n^2

1,2,4,8,16,32......--------an=2^(n-1)

[编辑本段]数列前N项和公式的求法

(一)1.等差数列:

通项公式an=a1+(n-1)d 首项a1,公差d, an第n项数

an=ak+(n-k)d ak为第k项数

若a,A,b构成等差数列 则 A=(a+b)/2

2.等差数列前n项和:

设等差数列的前n项和为Sn

即 Sn=a1+a2+...+an;

那么 Sn=na1+n(n-1)d/2

=dn^2(即n的2次方) /2+(a1-d/2)n

还有以下的求和方法: 1,不完全归纳法 2 累加法 3 倒序相加法

(二)1.等比数列:

通项公式 an=a1*q^(n-1)(即q的n-1次方) a1为首项,an为第n项

an=a1*q^(n-1),am=a1*q^(m-1)

则an/am=q^(n-m)

(1)an=am*q^(n-m)

(2)a,G,b 若构成等比中项,则G^2=ab (a,b,G不等于0)

(3)若m+n=p+q 则 am×an=ap×aq

2.等比数列前n项和